5.7: Analysis of Frames and Machines

Jacob Moore & Contributors
Pennsylvania State University Mont Alto via Mechanics Map

The process used to analyze frames and machines involves breaking the structure down into individual components in order to solve for the forces acting on each component. Sometimes the structure as a whole can be analyzed as a rigid body, and each component can always be analyzed as a rigid body.

The Process for Analyzing Frames and Machines:

In the beginning it is usually useful to label the members in your structure. This will help you keep everything organized and consistent in later analysis. In this book, we will label everything by assigning letters to each of the joints. 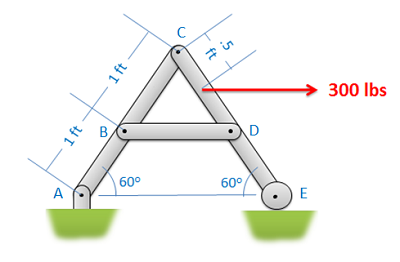force of 300 lbs is applied on beam CE, at the point 0.5 feet from point C." />
Next you will need to determine if we can analyze the entire structure as a rigid body. In order to do this, the structure needs to be independently rigid. This means that it would be rigid even if we separated it from its supports. If the structure is independently rigid (no machines, and only some frames, will be independently rigid), then analyze the structure as a single rigid body to determine the reaction forces acting on the structure. If the structure is not independently rigid, skip this step. 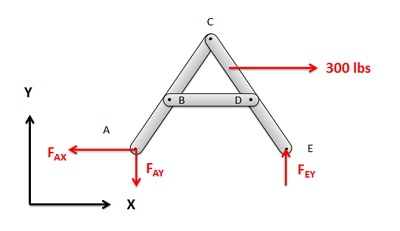$Free body diagram of the structure from Figure 1 above with the 300-lb applied force, using a standard-orientation $xy$-coordinate system. Reaction forces on point A are in the negative x and y directions, and point E experiences a reaction force in the positive y direction.$
Next you will draw a free body diagram for each of the components in the structure. You will need to include all forces acting on each member:
- First, add any external reaction or load forces that may be acting on the components.
- Second, identify any two-force members in the structure. At their connection points, they will cause a force with an unknown magnitude but a known direction (the forces will act along the line between the two connection points on the member).
- Next, add in the reaction forces (and possibly moments) at the connection points between non-two-force members. For forces with an unknown magnitude and direction (such as in pin joints), the forces are often drawn in as having unknown $x$ and $y$ components ($x$, $y$ and $z$ for 3D truss problems).
- Remember that the forces at each of the connection points will be a Newton's Third Law pair. This means that if one member exerts some force on some other member, then the second member will exert an equal and opposite force back on the first. When we draw out our unknown forces at the connection points, we must make sure that the forces acting on each member are opposite in direction.
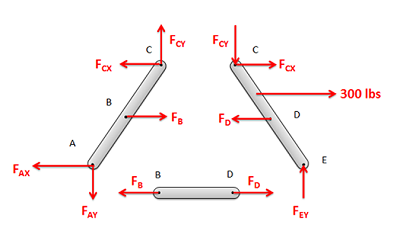
Write out the equilibrium equations for each component you drew a free body diagram of. These will be extended bodies, so you will need to write out the force and the moment equations.
- For 2D problems you will have three possible equations for each section: two force equations and one moment equation. \[ \sum \vec = 0 \quad\quad\quad\quad \sum \vec = 0 \] \[ \sum F_x = 0 \, ; \,\,\, \sum F_y = 0 \, ; \,\,\, \sum M_z = 0 \]
- For 3D problems you will have six possible equations for each section: three force equations and three moment equations. \[ \sum \vec = 0 \] \[ \sum F_x = 0 \, ; \,\,\, \sum F_y = 0 \, ; \,\,\, \sum F_z = 0 \] \[ \sum \vec = 0 \] \[ \sum M_x = 0 \, ; \,\,\, \sum M_y = 0 \, ; \,\,\, \sum M_z = 0 \]
Finally, solve the equilibrium equations for the unknowns. You can do this algebraically, solving for one variable at a time, or you can use matrix equations to solve for everything at once. If any force turns out to be negative, that indicates that the force actually travels in the opposite direction from what is indicated in your initial free body diagram.

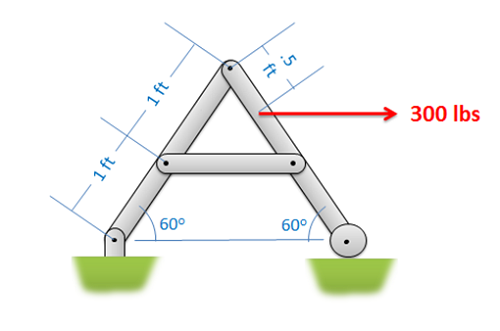An A-shaped structure with the two diagonal members each 2 feet long and at a 60° angle with the horizontal, and the horizontal member connecting the midpoints of each of the diagonal members. The bottom of the member on the left is attached to the ground with a pin joint, and the bottom of the member on the right is attached to the ground with a roller joint. A 300-lb rightwards force is applied to the member on the right, at a point 0.5 feet from the intersection of the two diagonal members.

Solution

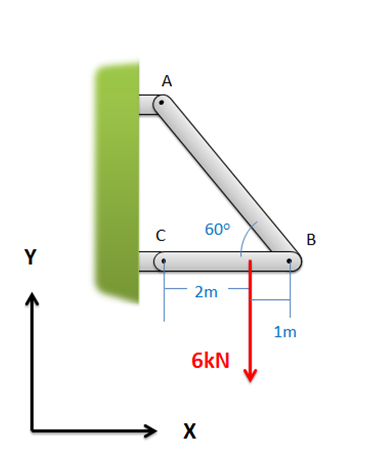The left end (point C) of a 3-meter horizontal beam is attached to a wall. A second beam makes a 60° angle with this beam, attaching to its right end (point B). Point A, the free end of the diagonal beam, is directly above point C and is attached to the same wall. A downwards force of 6 kN is applied at <a href=

the point on member BC, 1 meter left of point B." />Solution

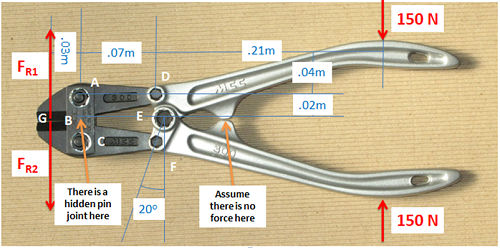Top-down view of a bolt cutter lying horizontally on a table, facing left. Its jaw adjustment bolts (A top, C bottom) are 0.04 m apart, and point B, midway between them, is the location of a hidden pin joint. Its middle bolts (D top, F bottom) are 0.07 m to the right of B, in line horizontally with A and C respectively. Its central bolt E, slightly to the right of D and F, is located at the intersection of the lines that pass through D and F at 20° from the vertical. The handles have a vertical force of 150 N each acting upon them, at the point 0.21 m right of and 0.04 m above/below point D/F, in the direction that compresses the handles. The reactive forces are depicted as 2 vertical vectors with their tails located at point G, which is 0.03 m left of point B.

Solution Side view of a rectangular tray on folding legs, appearing as a thin slab on top of an X. The tray is 3 feet off the ground and contains two joints 2 feet apart, each connecting to a diagonal leg; the legs intersect <a href=

Side view of a rectangular tray on folding legs, appearing as a thin slab on top of an X. The tray is 3 feet off the ground and contains two joints 2 feet apart, each connecting to a diagonal leg; the legs intersect <a href=

at a joint 1.5 feet of the ground and touch the ground at points 2 feet apart. A downwards 100-lb force is applied at the midpoint of the tray, halfway between its two joints." />Solution

Video $\PageIndex<5>$: Worked solution to example problem $\PageIndex$, provided by Dr. Jacob Moore. YouTube source: https://youtu.be/qi7WNDSb43k.

This page titled 5.7: Analysis of Frames and Machines is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Jacob Moore & Contributors (Mechanics Map) via source content that was edited to the style and standards of the LibreTexts platform.

Back to top
- 5.6: Frames and Machines
- 5.8: Chapter 5 Homework Problems

Was this article helpful?
Yes
No